Funciones y ecuaciones lineales

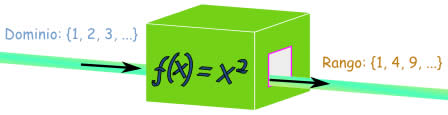
El geometrica  y e álgebra elemental , una función lineal es una funsion polinomica de primer grado; es decir, una función  cuya representación en el plano cartesiano  es una linea recta . Esta función se puede escribir como:

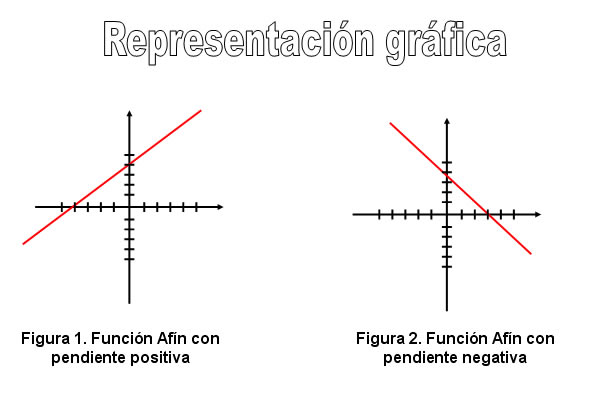
donde m y b son constantes reales  y x es una variable real. La constante m es la pendiente  de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.

Algunos autores llaman función lineal a aquella con b= 0 de la forma:

mientras que llaman función afín a la que tiene la forma:

cuando b es distinto de cero, dado que la primera (b=0) es un ejemplo también de transformación lineal, en el contexto de álgebra 

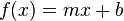
Funciones

El matemáticas , una función cuadrática o función de segundo grado es una función polinomica  definida por:

con .¹

Las gráficas  de estas funciones corresponden a parábolas  verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vértice  de la parábola  se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 el vértice se encuentra en la parte superior, siendo un máximo (es decir, la parábola se abre "hacia abajo").

El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre  el tiro parabólico 

La función derivada de una función cuadrática es una función lineal  y su integral indefinida es una familia de fusiones cubicas 

Dominio, codominio, recorrido y grafo de una función

Hay nombres especiales para lo que puede entrar, y también lo que puede salir de una función:

	Lo que puede entrar en una función se llama el dominio
	Lo que es posible que salga de una función se llama el codominio
	Lo que en realidad sale de una función se llama rango o imagen

Entonces, en el diagrama de arriba el conjunto "X" es el dominio, el conjunto "Y" es el codominio, y los elementos de Y a los que llegan flechas (los valores producidos realmente por la función) son el rango.

Parte de la función

Lo que sale (el rango) depende de lo que pones (el dominio), pero TÚ defines el dominio.

De hecho el dominio es una parte esencial de la función. Un dominio diferente da una función diferente.

Ejemplo: una simple función como f(x) = x² puede tener dominio (lo que entra) los números de contar {1,2,3,...}, y el rango será entonces el conjunto {1,4,9,...}

Formas para presentar una función

Funciones reales

unción real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real.

f : D    

   x      f(x) = y

El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por D.

El número x perteneciente al dominio de la función recibe el nombre de variable independiente.

Al número, y, asociado por f al valor x, se le llama variable dependiente. La imagen de x se designa por f(x). Luego

y= f(x)

Se denomina recorrido de una función al conjunto de los valores reales que toma la variable y o f(x).

Representación gráfica

Una gráfica es la representación en unos ejes de coordenadas de los pares ordenados de una tabla.

Las gráficas describen relaciones entre dos variables.

La variable que se representa en el eje horizontal se llama variable independiente o variable x.

La que se representa en el eje vertical se llama variable dependiente o variable y.

La variable y está en función de la variable x.

Una vez realizada la gráfica podemos estudiarla, analizarla y extraer conclusiones.

Para interpretar una gráfica, hemos de observarla de izquierda a derecha, analizando cómo varía la variable dependiente, y, al aumentar la variable independiente, x.

Kg de patatas	1	2	3	4	5
Precio en €	2	4	6	8	10

Función afín

Una función afín está definida por f(x)=mx+n, donde la variable es real, “m” y “n” son números reales. La representación gráfica de una función afín en el plano cartesiano es una recta.
La variable “m” representa la pendiente de la recta, la cual puede ser positiva (Figura 1) o negativa (Figura 2). La Variable “n” representa el corte con el eje “y”